Choco Solver

The Pareto Front in Choco Solver 4.0

Through this tutorial, we will focus on the optimization of two variables using the Pareto Front.

It consists on simultaneously optimize two incomparable variables.

We will use the Knapsack constraint, two optimize two decision variables : the quantity of glucose, and the quantity of lipids.

            
/*
 * Copyright (C) 2017 COSLING S.A.S.
 *
 * Licensed under the Apache License, Version 2.0 (the "License");
 * you may not use this file except in compliance with the License.
 * You may obtain a copy of the License at
 *
 *      http://www.apache.org/licenses/LICENSE-2.0
 *
 * Unless required by applicable law or agreed to in writing, software
 * distributed under the License is distributed on an "AS IS" BASIS,
 * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
 * See the License for the specific language governing permissions and
 * limitations under the License.
 */

import org.chocosolver.solver.Model;
import org.chocosolver.solver.Solution;
import org.chocosolver.solver.variables.IntVar;

import java.util.List;

/**
 * Simple Choco Solver example involving multi-objective optimization
 * @author Jean-Guillaume FAGES (cosling)
 * @version choco-solver-4.0.4
 */
public class Pareto {

    public static void main(String[] args) {
        // We handle 4 types of food, described below
        int[] nbItems = new int[]{5, 2, 6, 7}; // number of items for each type
        int[] weights = new int[]{5, 8, 7, 8}; // weight of an item for each type
        int[] lipids  = new int[]{5, 9, 8, 1}; // quantity of lipids of the item
        int[] glucose = new int[]{9, 5, 7, 32}; // quantity of glucose of the item

        Model model = new Model("ParetoKnapsack");

        // For each type, we create a variable for the number of occurrences
        IntVar[] occurrences = new IntVar[nbItems.length];
        for (int i = 0; i < nbItems.length; i++) {
            occurrences[i] = model.intVar(0, nbItems[i]);
        }

        // Total weight of the solution.
        IntVar weight = model.intVar(0, 80);
        // Total of lipids
        IntVar totalLipids = model.intVar(0, 200);
        // Total of glucose
        IntVar totalGlucose = model.intVar(0, 200);

        // We add two knapsack constraints to the solver
        // Beware : call the post() method to save it
        model.knapsack(occurrences, weight, totalLipids, weights, lipids).post();
        model.knapsack(occurrences, weight, totalGlucose, weights, glucose).post();

		// Optimise independently two variables using the Pareto optimizer
        List<Solution> solutions = model.getSolver().findParetoFront(new IntVar[]{totalLipids, totalGlucose},Model.MAXIMIZE);
        for (Solution solution : solutions) {
            System.out.println("-----------------------------------");
            System.out.println("W: " + solution.getIntVal(weight) + "\t G:" + solution.getIntVal(totalGlucose) + "\t L: " + solution.getIntVal(totalLipids));
            System.out.println("Strawberry jam: " + solution.getIntVal(occurrences[0]));
            System.out.println("Bananas: " + solution.getIntVal(occurrences[1]));
            System.out.println("Apples: " + solution.getIntVal(occurrences[2]));
            System.out.println("Honey: " + solution.getIntVal(occurrences[3]));
        }
        System.out.println("There are "+solutions.size()+" Pareto-optimal solutions");
    }
}
            
        

Once the main() method executed, a set of incomparable solutions is output. It is called the Pareto Front.

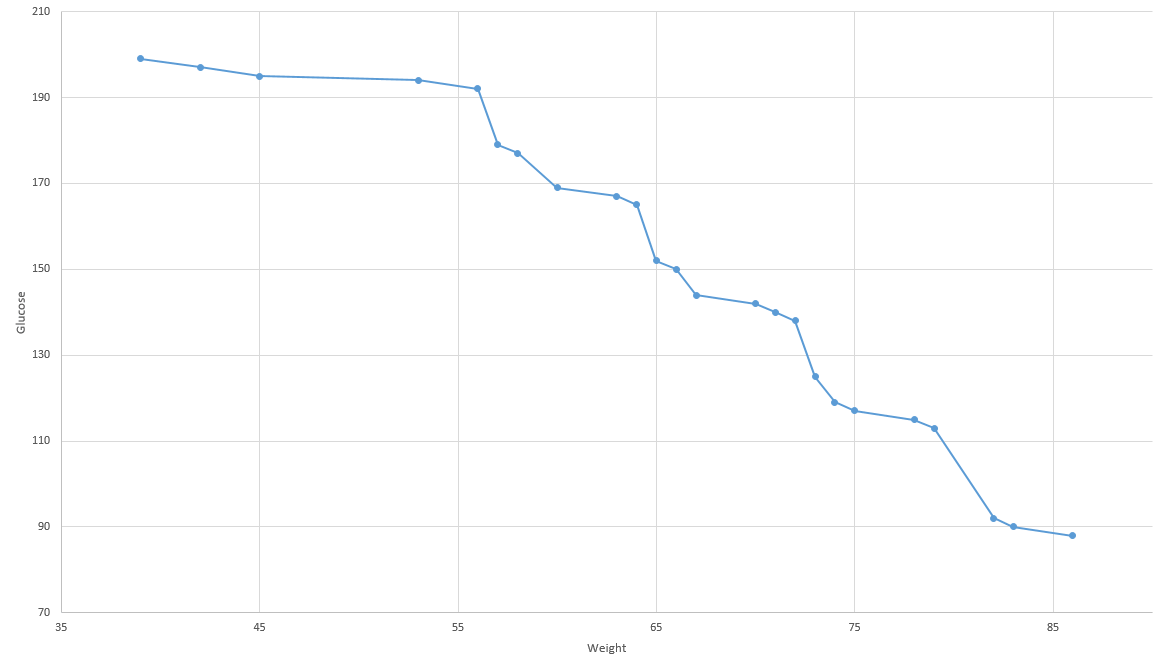
This chart represents all the solutions found by the Pareto Front, considering two decision variables to maximize. It doesn't exist any point such that its coordinates are better than any other point of the cloud.

3D generalisation

We now would like, in addition to maximising the total of glucose and lipids, minimize the total weight. Choco permits such an optimization, which we will do as follows :

        
// To minimize the weight in the same time, we take its opposite by using the choco's minus view
ParetoOptimizer pareto = new ParetoOptimizer(ResolutionPolicy.MAXIMIZE, new IntVar[]{totalLipids, totalGlucose, model.intMinusView(weight)});
model.getSolver().plugMonitor(pareto);
        
    

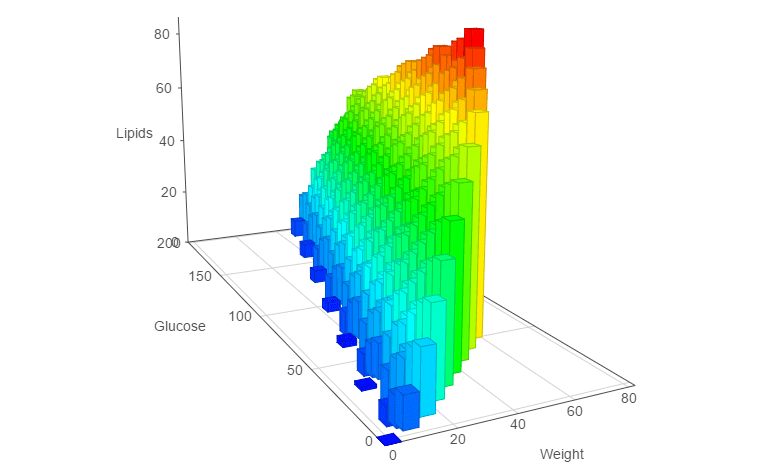
The Pareto Fronts becomes more complex : it is composed of 485 Pareto optimal solutions. We can represent it using a 3D surface.