Description du problème
Dans ce tutoriel, nous allons aborder l'optimisation de deux variables de décision, par l'intermédiaire du front de pareto. Le front de pareto consiste à optimiser parallèlement deux variables n'étant pas comparables. Pour l'example, nous allons ici aborder l'utilisation d'une contrainte Knapsack, où nous maximiserons deux variables de décision : la quantité de glucose et celle de lipides.Modélisation du problème
/*
* Copyright (C) 2017 COSLING S.A.S.
*
* Licensed under the Apache License, Version 2.0 (the "License");
* you may not use this file except in compliance with the License.
* You may obtain a copy of the License at
*
* http://www.apache.org/licenses/LICENSE-2.0
*
* Unless required by applicable law or agreed to in writing, software
* distributed under the License is distributed on an "AS IS" BASIS,
* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
* See the License for the specific language governing permissions and
* limitations under the License.
*/
import org.chocosolver.solver.Model;
import org.chocosolver.solver.Solution;
import org.chocosolver.solver.variables.IntVar;
import java.util.List;
/**
* Simple Choco Solver example involving multi-objective optimization
* @author Jean-Guillaume FAGES (cosling)
* @version choco-solver-4.0.4
*/
public class Pareto {
public static void main(String[] args) {
// We handle 4 types of food, described below
int[] nbItems = new int[]{5, 2, 6, 7}; // number of items for each type
int[] weights = new int[]{5, 8, 7, 8}; // weight of an item for each type
int[] lipids = new int[]{5, 9, 8, 1}; // quantity of lipids of the item
int[] glucose = new int[]{9, 5, 7, 32}; // quantity of glucose of the item
Model model = new Model("ParetoKnapsack");
// For each type, we create a variable for the number of occurrences
IntVar[] occurrences = new IntVar[nbItems.length];
for (int i = 0; i < nbItems.length; i++) {
occurrences[i] = model.intVar(0, nbItems[i]);
}
// Total weight of the solution.
IntVar weight = model.intVar(0, 80);
// Total of lipids
IntVar totalLipids = model.intVar(0, 200);
// Total of glucose
IntVar totalGlucose = model.intVar(0, 200);
// We add two knapsack constraints to the solver
// Beware : call the post() method to save it
model.knapsack(occurrences, weight, totalLipids, weights, lipids).post();
model.knapsack(occurrences, weight, totalGlucose, weights, glucose).post();
// Optimise independently two variables using the Pareto optimizer
List<Solution> solutions = model.getSolver().findParetoFront(new IntVar[]{totalLipids, totalGlucose},Model.MAXIMIZE);
for (Solution solution : solutions) {
System.out.println("-----------------------------------");
System.out.println("W: " + solution.getIntVal(weight) + "\t G:" + solution.getIntVal(totalGlucose) + "\t L: " + solution.getIntVal(totalLipids));
System.out.println("Strawberry jam: " + solution.getIntVal(occurrences[0]));
System.out.println("Bananas: " + solution.getIntVal(occurrences[1]));
System.out.println("Apples: " + solution.getIntVal(occurrences[2]));
System.out.println("Honey: " + solution.getIntVal(occurrences[3]));
}
System.out.println("There are "+solutions.size()+" Pareto-optimal solutions");
}
}
Résolution du problème
Une fois la méthode main() exécutée, nous obtenons un ensemble de solutions (le front de Pareto) incomparables.
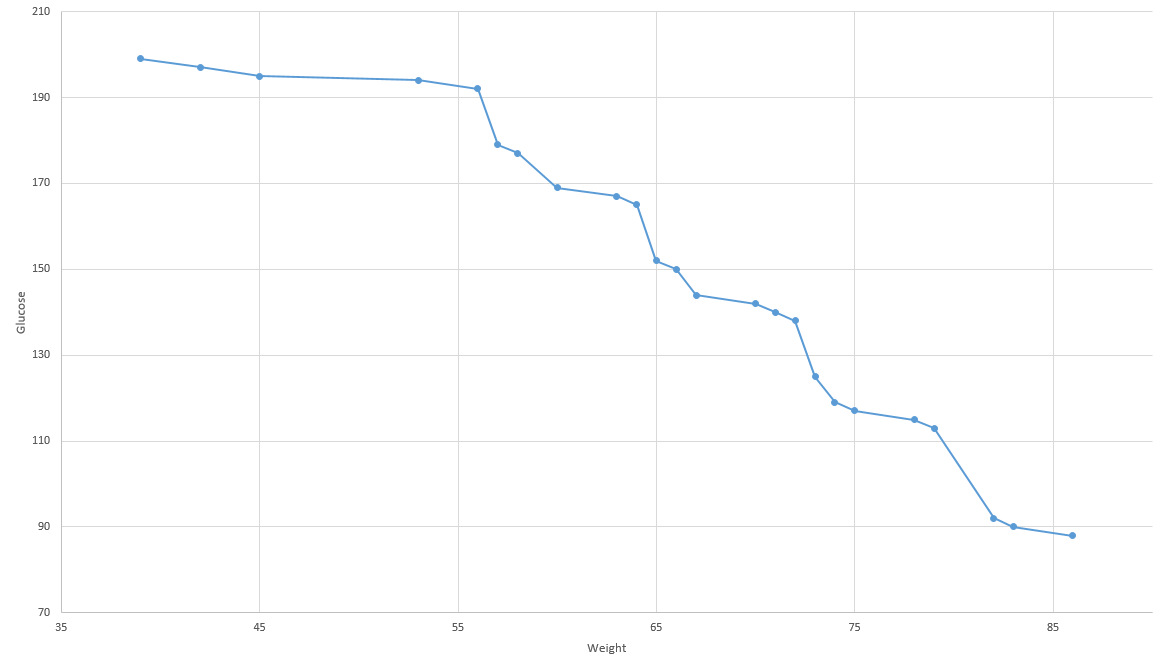
Ce graphique représente la totalité des solutions trouvées par l'intermédiaire du front de Pareto, considérant nos deux dimensions à optimiser. On remarque ici qu'il n'existe pas de point tel que ses deux coordonnées sont meilleures qu'un autre point du nuage. C'est le principe du front de pareto.
Généralisation 3D
Nous voulons maintenant, en plus de maximiser le total de glucoses et de lipides, minimiser le poids total. Choco Solver permet une telle optimisation, qu'on effectuera de la manière suivante :
// To minimize the weight in the same time, we take its opposite by using the choco's minus view
ParetoOptimizer pareto = new ParetoOptimizer(ResolutionPolicy.MAXIMIZE, new IntVar[]{totalLipids, totalGlucose, model.intMinusView(weight)});
model.getSolver().plugMonitor(pareto);
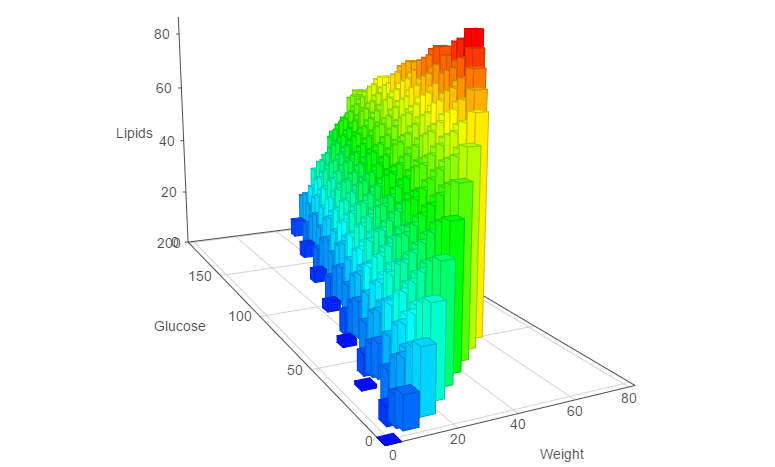
Le front de Pareto devient plus complexe : il est composé de 485 solutions optimales au sens de Pareto, ce qu'on peut représenter en trois dimensions par l'intermédiaire d'une surface.