Description du problème
Etant donné un graphe non-orienté, un ensemble dominant est un sous-ensemble de noeuds tel que chaque noeud du graphe peut-être connecté à ce sous-ensemble par au plus une arrête. Dans cet exemple nous cherchons un ensemble dominant de cardinalité minimale et tel que le sous-graphe induit par cet ensemble soit connexe. Le code générant le graphe d'entrée est donné ci-dessous :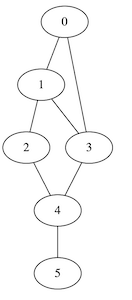
Graphe d'entrée
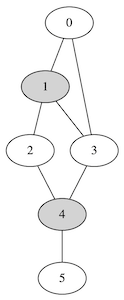
Ensemble dominant non-connexe
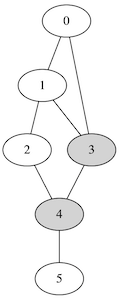
Ensemble dominant connexe
/**
* Creates an undirected graph of 6 nodes and 7 edges
* @return an UndirectedGraph
*/
private static UndirectedGraph createInputGraph() {
// creates a graph with 6 nodes (from 0 to 5)
UndirectedGraph inputGraph = new UndirectedGraph(6, SetType.BITSET, true);
// add 7 edges
int[][] edges = {{0, 1}, {1, 2}, {0, 3}, {1, 3}, {2, 4}, {3, 4}, {4, 5}};
Arrays.stream(edges).forEach(edge -> inputGraph.addEdge(edge[0], edge[1]));
return inputGraph;
}
UndirectedGraph inputGraph = createInputGraph();
System.out.println("input graph compact representation: \n" + inputGraph);
System.out.println("input graph graphviz representation:\n" + inputGraph.graphVizExport());
Modélisation du problème
Création d'une variable de graphe
Modélisons maintenant ce problème avec Choco Solver. Nous créons une variable de graphe pour représenter la recherche d'un sous-graphe du graphe d'entrée donnée. Pour cela, nous définissons une borne inférieure : un graphe vide ; et une borne supérieure : le graphe d'entrée. Toute valeur de la variable devra être comprise entre ces deux bornes.
/**
* Create a graph variable representing an induced subgraph of inputGraph
* @param model a choco-solver Model
* @param inputGraph an undirected graph defining the variable's upper bound
* @return an UndirectedGraphVar
*/
private static UndirectedGraphVar createGraphVariable(Model model, UndirectedGraph inputGraph) {
int n = inputGraph.getNbMaxNodes();
// --- graph lower bound : an empty graph
UndirectedGraph GLB = new UndirectedGraph(model, n, SetType.BITSET, false);
UndirectedGraph GUB = new UndirectedGraph(model, n, SetType.BITSET, false);
for (int i : inputGraph.getNodes()) {
GUB.addNode(i); // all nodes are possible
for (int j : inputGraph.getNeighborsOf(i)) {
GUB.addEdge(i, j); // all edges of inputGraph are possible
}
}
// create a graph variable with domain [GLB, GUB]
// any of its value will be a supergraph of GLB and a subgraph of GUB
return model.graphVar("g", GLB, GUB);
}
Contrainte de connexité
La contrainte de connexité est assurée par une contrainte globale dédiée, nommée connected. Cette contrainte embarque des algorithmes de graphe efficaces et évite une reformulation coûteuse.
// --- Connectivity constraint : the graph variable must be connected
model.connected(subgraph).post();
Représentation booléenne des noeuds du graphe
Afin de simplifier le reste de la modélisation, nous introduisons une représentation duale, basée sur des variables booléenne.
// DOMINATING SET
// --- one boolean variable per node
BoolVar[] domSet = model.boolVarArray(n);
model.nodesChanneling(subgraph, domSet).post();
Chaque noeud du graphe est ainsi relié à une variable binaire. Puisque les véritables variables de décisions sont les noeuds du graphe, et non ses arrêtes, it sera plus commode pour le branchement de raisonner sur les variables binaires. La variable de graphe n’est alors plus qu’un support à la contrainte globale de connexité mais ne constitue plus une variable de décision: il n'est pas nécessaire de brancher sur les arcs du graphe.
Contraintes de couverture
Les contraintes de couvertures sont exprimées au moyen de contraintes logique (OR) sur les variables booléennes.
// --- covering constraints
// (each node should be either dominating or a direct neighbor of a dominating node)
for (int i = 0; i < n; i++) {
int idx = 0;
BoolVar[] cluster = new BoolVar[1 + inputGraph.getNeighborsOf(i).size()];
cluster[idx++] = domSet[i];
for (int j : inputGraph.getNeighborsOf(i)) {
cluster[idx++] = domSet[j];
}
model.or(cluster).post();
}
Minimisation de la cardinalité de l'ensemble dominant
La fonction objectif consiste à minimiser le nombre de noeuds, soit la somme des variables binaires associées aux noeuds du graphe. Il est également possible de faire appel à la contrainte nbNodes
// --- minimize the number of nodes in the dominating set
IntVar size = model.sum("nbNodes", domSet);
model.setObjective(Model.MINIMIZE, size);
Résolution du problème
Heuristique de recherche
Nous pouvons préciser une heuristique visant à retirer d’abord les noeuds de faible degré. Cela permettra a priori d’avoir une bonne première solution. Nous trions donc les variables binaires par ordre croissant de nombre de voisins dans le graphe d'entrée. Le choix de valeur consiste à choisir la borne inférieure, ce qui correspond à retirer des noeuds du graphe.
// --- sort nodes by increasing neighborhood size
BoolVar[] orderedDomVar = IntStream.range(0, n)
.boxed()
.sorted(Comparator.comparingInt(i -> inputGraph.getNeighborsOf(i).size()))
.map(i -> domSet[i])
.toArray(BoolVar[]::new);
model.getSolver().setSearch(Search.inputOrderLBSearch(orderedDomVar));
Exécution du modèle
Une fois les contraintes et la fonction objectif posée, la recherche de solutions améliorantes peut être appelée via la méthode solve du solveur. Ici, la première solution est optimale.
// SOLVING
System.out.println("start solving...");
while (model.getSolver().solve()) {
int[] solution = IntStream.range(0, n).filter(i -> domSet[i].isInstantiatedTo(1)).toArray();
System.out.println("dominating set : " + Arrays.toString(solution));
}
Sortie console :
input graph compact representation:
nodes :
[0,5]
neighbors :
0 -> {1 3 }
1 -> {0 2 3 }
2 -> {1 4 }
3 -> {0 1 4 }
4 -> {2 3 5 }
5 -> {4 }
input graph graphviz representation:
graph G{
0 1 2 3 4 5 ;
0 -- 1 ;
0 -- 3 ;
1 -- 2 ;
1 -- 3 ;
2 -- 4 ;
3 -- 4 ;
4 -- 5 ;
}
start solving...
dominating set : [3, 4]
Model[Model-0], 1 Solutions, MINIMIZE nbNodes = 2, Resolution time 0,023s, Time to best solution 0,002s, 5 Nodes (213,0 n/s), 0 Backtracks, 0 Backjumps, 0 Fails, 0 Restarts
** Choco 4.10.14 (2023-11) : Constraint Programming Solver, Copyright (c) 2010-2023
- Model[Model-0] features:
Variables : 14
Constraints : 15
Building time : 0,047s
User-defined search strategy : yes
Complementary search strategy : no
- Complete search - 1 solution found.
Model[Model-0]
Solutions: 1
MINIMIZE nbNodes = 2,
Building time : 0,047s
Resolution time : 0,028s
Time to best solution : 0,002s
Nodes: 5 (180,5 n/s)
Backtracks: 9
Backjumps: 0
Fails: 4
Restarts: 0
Code complet
/*
* Copyright (C) 2025 COSLING S.A.S.
*
* Licensed under the Apache License, Version 2.0 (the "License");
* you may not use this file except in compliance with the License.
* You may obtain a copy of the License at
*
* http://www.apache.org/licenses/LICENSE-2.0
*
* Unless required by applicable law or agreed to in writing, software
* distributed under the License is distributed on an "AS IS" BASIS,
* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
* See the License for the specific language governing permissions and
* limitations under the License.
*/
package com.cosling.tutorials;
import org.chocosolver.solver.Model;
import org.chocosolver.solver.search.strategy.Search;
import org.chocosolver.solver.variables.BoolVar;
import org.chocosolver.solver.variables.IntVar;
import org.chocosolver.solver.variables.UndirectedGraphVar;
import org.chocosolver.util.objects.graphs.UndirectedGraph;
import org.chocosolver.util.objects.setDataStructures.SetType;
import java.util.Arrays;
import java.util.Comparator;
import java.util.stream.IntStream;
/**
* Simple example of connected dominating set problem
* Shows how to use graph-set channeling and how to create a set constraint
* @author Jean-Guillaume FAGES (cosling)
* @version Choco Solver 4.10.14
*/
public class DomSetProblem {
public static void main(String[] args) {
// INPUT GRAPH --- Generation
UndirectedGraph inputGraph = createInputGraph();
int n = inputGraph.getNbMaxNodes(); // number of nodes
// print input graph as graphviz format to display it on http://www.webgraphviz.com/
System.out.println("input graph compact representation: \n" + inputGraph);
System.out.println("input graph graphviz representation:\n"
+ inputGraph.graphVizExport());
Model model = new Model();
// GRAPH VARIABLE : initial domain (from https://en.wikipedia.org/wiki/Dominating_set)
UndirectedGraphVar subgraph = createGraphVariable(model, inputGraph);
// --- Connectivity constraint : the graph variable must be connected
model.connected(subgraph).post();
// DOMINATING SET
// --- one boolean variable per node
BoolVar[] domSet = model.boolVarArray(n);
model.nodesChanneling(subgraph, domSet).post();
// --- minimize the number of nodes in the dominating set
IntVar size = model.sum("nbNodes", domSet);
model.setObjective(Model.MINIMIZE, size);
// --- covering constraints
// (each node should be either dominating or a direct neighbor of a dominating node)
for (int i = 0; i < n; i++) {
int idx = 0;
BoolVar[] cluster = new BoolVar[1 + inputGraph.getNeighborsOf(i).size()];
cluster[idx++] = domSet[i];
for (int j : inputGraph.getNeighborsOf(i)) {
cluster[idx++] = domSet[j];
}
model.or(cluster).post();
}
// SEARCH
// --- sort nodes by increasing neighborhood size
BoolVar[] orderedDomVar = IntStream.range(0, n)
.boxed()
.sorted(Comparator.comparingInt(i -> inputGraph.getNeighborsOf(i).size()))
.map(i -> domSet[i])
.toArray(BoolVar[]::new);
model.getSolver().setSearch(Search.inputOrderLBSearch(orderedDomVar));
// SOLVING
System.out.println("start solving...");
while (model.getSolver().solve()) {
int[] solution = IntStream.range(0, n).filter(i -> domSet[i].isInstantiatedTo(1)).toArray();
System.out.println("dominating set : " + Arrays.toString(solution));
System.out.println(model.getSolver().toOneLineString());
}
model.getSolver().printStatistics();
}
/**
* Creates an undirected graph of 6 nodes and 7 edges
*
* @return an UndirectedGraph
*/
private static UndirectedGraph createInputGraph() {
// creates a graph with 6 nodes (from 0 to 5)
UndirectedGraph inputGraph = new UndirectedGraph(6, SetType.BITSET, true);
// add 7 edges
int[][] edges = {{0, 1}, {1, 2}, {0, 3}, {1, 3}, {2, 4}, {3, 4}, {4, 5}};
Arrays.stream(edges).forEach(edge -> inputGraph.addEdge(edge[0], edge[1]));
return inputGraph;
}
/**
* Create a graph variable representing an induced subgraph of inputGraph
*
* @param model a choco-solver Model
* @param inputGraph an undirected graph defining the variable's upper bound
* @return an UndirectedGraphVar
*/
private static UndirectedGraphVar createGraphVariable(Model model, UndirectedGraph inputGraph) {
int n = inputGraph.getNbMaxNodes();
// --- graph lower bound : an empty graph
UndirectedGraph GLB = new UndirectedGraph(model, n, SetType.BITSET, false);
UndirectedGraph GUB = new UndirectedGraph(model, n, SetType.BITSET, false);
for (int i : inputGraph.getNodes()) {
GUB.addNode(i); // all nodes are possible
for (int j : inputGraph.getNeighborsOf(i)) {
GUB.addEdge(i, j); // all edges of inputGraph are possible
}
}
// create a graph variable with domain [GLB, GUB]
// any of its value will be a supergraph of GLB and a subgraph of GUB
return model.graphVar("g", GLB, GUB);
}
}