Cálculo de un Frente de Pareto con Choco Solver 4.0

Descripción del problema

En este tutorial, vamos a abordar la optimización de dos variables de decisión, mediante el frente de pareto. El frente de pareto consiste en optimizar paralelamente dos variables que no son comparables. Para el ejemplo, vamos aquí a abordar el uso de una restricción Knapsack, donde maximizaremos dos variables de decisión: la cantidad de glucosa y la de lípidos.

Modelización del problema

            
 /*
 * Copyright (C) 2017 COSLING S.A.S.
 *
 * Licensed under the Apache License, Version 2.0 (the "License");
 * you may not use this file except in compliance with the License.
 * You may obtain a copy of the License at
 *
 *      http://www.apache.org/licenses/LICENSE-2.0
 *
 * Unless required by applicable law or agreed to in writing, software
 * distributed under the License is distributed on an "AS IS" BASIS,
 * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
 * See the License for the specific language governing permissions and
 * limitations under the License.
 */

import org.chocosolver.solver.Model;
import org.chocosolver.solver.Solution;
import org.chocosolver.solver.variables.IntVar;

import java.util.List;

/**
 * Simple Choco Solver example involving multi-objective optimization
 * @author Jean-Guillaume FAGES (cosling)
 * @version choco-solver-4.0.4
 */
public class Pareto {

    public static void main(String[] args) {
        // We handle 4 types of food, described below
        int[] nbItems = new int[]{5, 2, 6, 7}; // number of items for each type
        int[] weights = new int[]{5, 8, 7, 8}; // weight of an item for each type
        int[] lipids  = new int[]{5, 9, 8, 1}; // quantity of lipids of the item
        int[] glucose = new int[]{9, 5, 7, 32}; // quantity of glucose of the item

        Model model = new Model("ParetoKnapsack");

        // For each type, we create a variable for the number of occurrences
        IntVar[] occurrences = new IntVar[nbItems.length];
        for (int i = 0; i < nbItems.length; i++) {
            occurrences[i] = model.intVar(0, nbItems[i]);
        }

        // Total weight of the solution.
        IntVar weight = model.intVar(0, 80);
        // Total of lipids
        IntVar totalLipids = model.intVar(0, 200);
        // Total of glucose
        IntVar totalGlucose = model.intVar(0, 200);

        // We add two knapsack constraints to the solver
        // Beware : call the post() method to save it
        model.knapsack(occurrences, weight, totalLipids, weights, lipids).post();
        model.knapsack(occurrences, weight, totalGlucose, weights, glucose).post();

		// Optimise independently two variables using the Pareto optimizer
        List<Solution> solutions = model.getSolver().findParetoFront(new IntVar[]{totalLipids, totalGlucose},Model.MAXIMIZE);
        for (Solution solution : solutions) {
            System.out.println("-----------------------------------");
            System.out.println("W: " + solution.getIntVal(weight) + "\t G:" + solution.getIntVal(totalGlucose) + "\t L: " + solution.getIntVal(totalLipids));
            System.out.println("Strawberry jam: " + solution.getIntVal(occurrences[0]));
            System.out.println("Bananas: " + solution.getIntVal(occurrences[1]));
            System.out.println("Apples: " + solution.getIntVal(occurrences[2]));
            System.out.println("Honey: " + solution.getIntVal(occurrences[3]));
        }
        System.out.println("There are "+solutions.size()+" Pareto-optimal solutions");
    }
}
            
        

Resolución del problema

Una vez ejecutado el método main(), obtenemos un conjunto de soluciones (el frente de Pareto) incomparables.

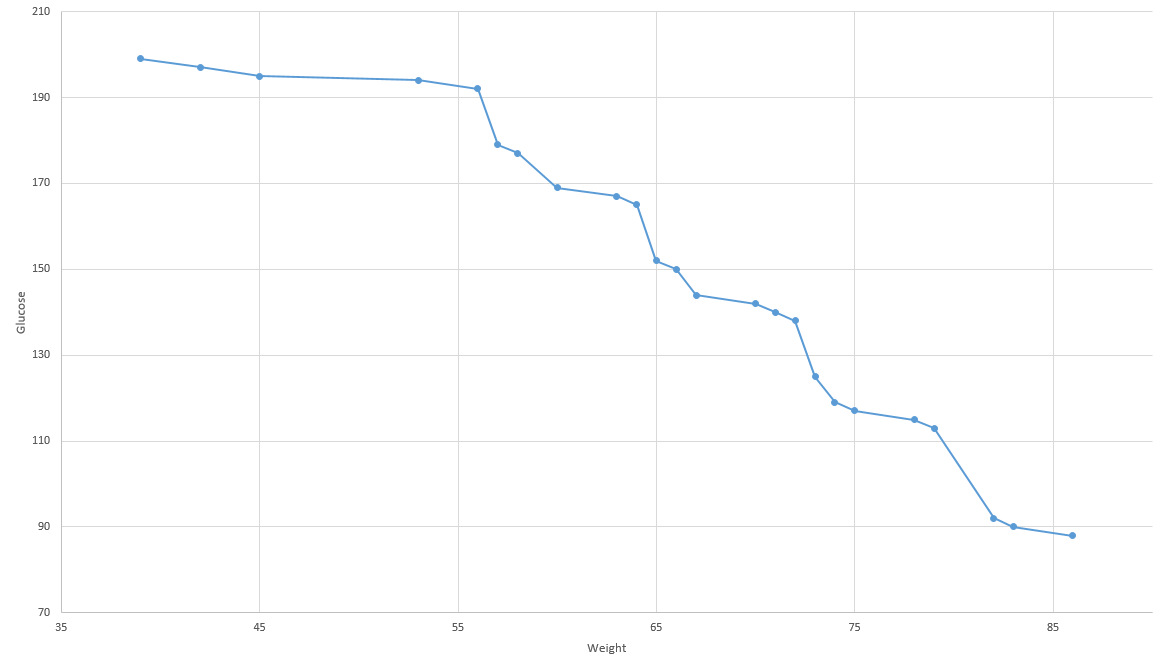
Este gráfico representa la totalidad de las soluciones encontradas mediante el frente de Pareto, considerando nuestras dos dimensiones a optimizar. Se observa aquí que no existe un punto tal que sus dos coordenadas sean mejores que otro punto de la nube. Este es el principio del frente de pareto.

Generalización 3D

Queremos ahora, además de maximizar el total de glucosas y de lípidos, minimizar el peso total. Choco Solver permite tal optimización, que efectuaremos de la manera siguiente:

            
// To minimize the weight in the same time, we take its opposite by using the choco's minus view
ParetoOptimizer pareto = new ParetoOptimizer(ResolutionPolicy.MAXIMIZE, new IntVar[]{totalLipids, totalGlucose, model.intMinusView(weight)});
model.getSolver().plugMonitor(pareto);
            
        

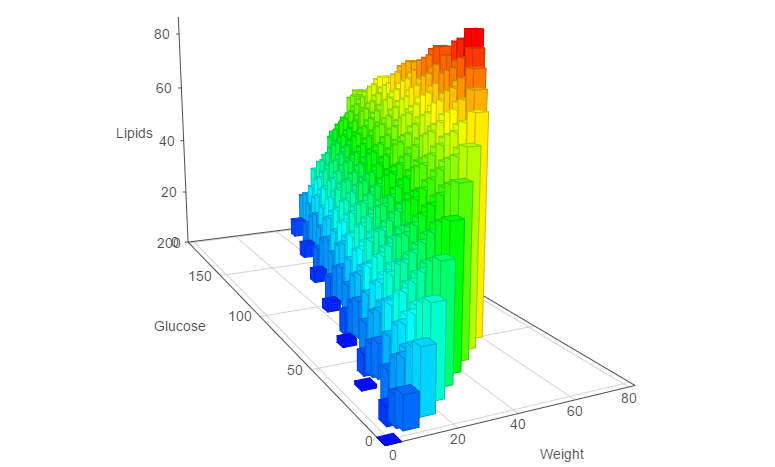
El frente de Pareto se vuelve más complejo: está compuesto de 485 soluciones óptimas en el sentido de Pareto, lo que se puede representar en tres dimensiones mediante una superficie.