Descripción del problema
Dado un grafo no-orientado, un conjunto dominante es un subconjunto de nodos tal que cada nodo del grafo puede estar conectado a este subconjunto por como máximo una arista. En este ejemplo buscamos un conjunto dominante de cardinalidad mínima y tal que el subgrafo inducido por este conjunto sea conexo. El código que genera el grafo de entrada se da a continuación: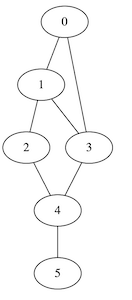
Grafo de entrada
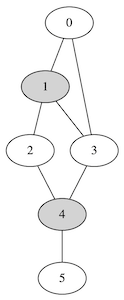
Conjunto dominante no-conexo
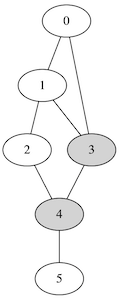
Conjunto dominante conexo
/**
* Creates an undirected graph of 6 nodes and 7 edges
* @return an UndirectedGraph
*/
private static UndirectedGraph createInputGraph() {
// creates a graph with 6 nodes (from 0 to 5)
UndirectedGraph inputGraph = new UndirectedGraph(6, SetType.BITSET, true);
// add 7 edges
int[][] edges = {{0, 1}, {1, 2}, {0, 3}, {1, 3}, {2, 4}, {3, 4}, {4, 5}};
Arrays.stream(edges).forEach(edge -> inputGraph.addEdge(edge[0], edge[1]));
return inputGraph;
}
UndirectedGraph inputGraph = createInputGraph();
System.out.println("input graph compact representation: \n" + inputGraph);
System.out.println("input graph graphviz representation:\n" + inputGraph.graphVizExport());
Modelización del problema
Creación de una variable de grafo
Modelemos ahora este problema con Choco Solver. Creamos una variable de grafo para representar la búsqueda de un subgrafo del grafo de entrada dado. Para esto, definimos una cota inferior: un grafo vacío; y una cota superior: el grafo de entrada. Todo valor de la variable deberá estar comprendido entre estas dos cotas.
/**
* Create a graph variable representing an induced subgraph of inputGraph
* @param model a choco-solver Model
* @param inputGraph an undirected graph defining the variable's upper bound
* @return an UndirectedGraphVar
*/
private static UndirectedGraphVar createGraphVariable(Model model, UndirectedGraph inputGraph) {
int n = inputGraph.getNbMaxNodes();
// --- graph lower bound : an empty graph
UndirectedGraph GLB = new UndirectedGraph(model, n, SetType.BITSET, false);
UndirectedGraph GUB = new UndirectedGraph(model, n, SetType.BITSET, false);
for (int i : inputGraph.getNodes()) {
GUB.addNode(i); // all nodes are possible
for (int j : inputGraph.getNeighborsOf(i)) {
GUB.addEdge(i, j); // all edges of inputGraph are possible
}
}
// create a graph variable with domain [GLB, GUB]
// any of its value will be a supergraph of GLB and a subgraph of GUB
return model.graphVar("g", GLB, GUB);
}
Restricción de conexidad
La restricción de conexidad se asegura mediante una restricción global dedicada, denominada connected. Esta restricción embarca algoritmos de grafo eficaces y evita una reformulación costosa.
// --- Connectivity constraint : the graph variable must be connected
model.connected(subgraph).post();
Representación booleana de los nodos del grafo
Para simplificar el resto de la modelización, introducimos una representación dual, basada en variables booleanas.
// DOMINATING SET
// --- one boolean variable per node
BoolVar[] domSet = model.boolVarArray(n);
model.nodesChanneling(subgraph, domSet).post();
Cada nodo del grafo está así relacionado con una variable binaria. Puesto que las verdaderas variables de decisión son los nodos del grafo, y no sus aristas, será más cómodo para la ramificación razonar sobre las variables binarias. La variable de grafo ya no es entonces más que un soporte para la restricción global de conexidad pero ya no constituye una variable de decisión: no es necesario ramificar sobre los arcos del grafo.
Restricciones de cobertura
Las restricciones de cobertura se expresan mediante restricciones lógicas (OR) sobre las variables booleanas.
// --- covering constraints
// (each node should be either dominating or a direct neighbor of a dominating node)
for (int i = 0; i < n; i++) {
int idx = 0;
BoolVar[] cluster = new BoolVar[1 + inputGraph.getNeighborsOf(i).size()];
cluster[idx++] = domSet[i];
for (int j : inputGraph.getNeighborsOf(i)) {
cluster[idx++] = domSet[j];
}
model.or(cluster).post();
}
Minimización de la cardinalidad del conjunto dominante
La función objetivo consiste en minimizar el número de nodos, es decir la suma de las variables binarias asociadas a los nodos del grafo. También es posible hacer uso de la restricción nbNodes
// --- minimize the number of nodes in the dominating set
IntVar size = model.sum("nbNodes", domSet);
model.setObjective(Model.MINIMIZE, size);
Resolución del problema
Heurística de búsqueda
Podemos precisar una heurística que apunte a retirar primero los nodos de grado bajo. Esto permitirá a priori tener una buena primera solución. Ordenamos por tanto las variables binarias por orden creciente de número de vecinos en el grafo de entrada. La elección de valor consiste en elegir la cota inferior, lo que corresponde a retirar nodos del grafo.
// --- sort nodes by increasing neighborhood size
BoolVar[] orderedDomVar = IntStream.range(0, n)
.boxed()
.sorted(Comparator.comparingInt(i -> inputGraph.getNeighborsOf(i).size()))
.map(i -> domSet[i])
.toArray(BoolVar[]::new);
model.getSolver().setSearch(Search.inputOrderLBSearch(orderedDomVar));
Ejecución del modelo
Una vez publicadas las restricciones y la función objetivo, la búsqueda de soluciones mejoradas puede ser llamada mediante el método solve del solucionador. Aquí, la primera solución es óptima.
// SOLVING
System.out.println("start solving...");
while (model.getSolver().solve()) {
int[] solution = IntStream.range(0, n).filter(i -> domSet[i].isInstantiatedTo(1)).toArray();
System.out.println("dominating set : " + Arrays.toString(solution));
}
Salida consola:
input graph compact representation:
nodes :
[0,5]
neighbors :
0 -> {1 3 }
1 -> {0 2 3 }
2 -> {1 4 }
3 -> {0 1 4 }
4 -> {2 3 5 }
5 -> {4 }
input graph graphviz representation:
graph G{
0 1 2 3 4 5 ;
0 -- 1 ;
0 -- 3 ;
1 -- 2 ;
1 -- 3 ;
2 -- 4 ;
3 -- 4 ;
4 -- 5 ;
}
start solving...
dominating set : [3, 4]
Model[Model-0], 1 Solutions, MINIMIZE nbNodes = 2, Resolution time 0,023s, Time to best solution 0,002s, 5 Nodes (213,0 n/s), 0 Backtracks, 0 Backjumps, 0 Fails, 0 Restarts
** Choco 4.10.14 (2023-11) : Constraint Programming Solver, Copyright (c) 2010-2023
- Model[Model-0] features:
Variables : 14
Constraints : 15
Building time : 0,047s
User-defined search strategy : yes
Complementary search strategy : no
- Complete search - 1 solution found.
Model[Model-0]
Solutions: 1
MINIMIZE nbNodes = 2,
Building time : 0,047s
Resolution time : 0,028s
Time to best solution : 0,002s
Nodes: 5 (180,5 n/s)
Backtracks: 9
Backjumps: 0
Fails: 4
Restarts: 0
Código completo
/*
* Copyright (C) 2025 COSLING S.A.S.
*
* Licensed under the Apache License, Version 2.0 (the "License");
* you may not use this file except in compliance with the License.
* You may obtain a copy of the License at
*
* http://www.apache.org/licenses/LICENSE-2.0
*
* Unless required by applicable law or agreed to in writing, software
* distributed under the License is distributed on an "AS IS" BASIS,
* WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
* See the License for the specific language governing permissions and
* limitations under the License.
*/
package com.cosling.tutorials;
import org.chocosolver.solver.Model;
import org.chocosolver.solver.search.strategy.Search;
import org.chocosolver.solver.variables.BoolVar;
import org.chocosolver.solver.variables.IntVar;
import org.chocosolver.solver.variables.UndirectedGraphVar;
import org.chocosolver.util.objects.graphs.UndirectedGraph;
import org.chocosolver.util.objects.setDataStructures.SetType;
import java.util.Arrays;
import java.util.Comparator;
import java.util.stream.IntStream;
/**
* Simple example of connected dominating set problem
* Shows how to use graph-set channeling and how to create a set constraint
* @author Jean-Guillaume FAGES (cosling)
* @version Choco Solver 4.10.14
*/
public class DomSetProblem {
public static void main(String[] args) {
// INPUT GRAPH --- Generation
UndirectedGraph inputGraph = createInputGraph();
int n = inputGraph.getNbMaxNodes(); // number of nodes
// print input graph as graphviz format to display it on http://www.webgraphviz.com/
System.out.println("input graph compact representation: \n" + inputGraph);
System.out.println("input graph graphviz representation:\n"
+ inputGraph.graphVizExport());
Model model = new Model();
// GRAPH VARIABLE : initial domain (from https://en.wikipedia.org/wiki/Dominating_set)
UndirectedGraphVar subgraph = createGraphVariable(model, inputGraph);
// --- Connectivity constraint : the graph variable must be connected
model.connected(subgraph).post();
// DOMINATING SET
// --- one boolean variable per node
BoolVar[] domSet = model.boolVarArray(n);
model.nodesChanneling(subgraph, domSet).post();
// --- minimize the number of nodes in the dominating set
IntVar size = model.sum("nbNodes", domSet);
model.setObjective(Model.MINIMIZE, size);
// --- covering constraints
// (each node should be either dominating or a direct neighbor of a dominating node)
for (int i = 0; i < n; i++) {
int idx = 0;
BoolVar[] cluster = new BoolVar[1 + inputGraph.getNeighborsOf(i).size()];
cluster[idx++] = domSet[i];
for (int j : inputGraph.getNeighborsOf(i)) {
cluster[idx++] = domSet[j];
}
model.or(cluster).post();
}
// SEARCH
// --- sort nodes by increasing neighborhood size
BoolVar[] orderedDomVar = IntStream.range(0, n)
.boxed()
.sorted(Comparator.comparingInt(i -> inputGraph.getNeighborsOf(i).size()))
.map(i -> domSet[i])
.toArray(BoolVar[]::new);
model.getSolver().setSearch(Search.inputOrderLBSearch(orderedDomVar));
// SOLVING
System.out.println("start solving...");
while (model.getSolver().solve()) {
int[] solution = IntStream.range(0, n).filter(i -> domSet[i].isInstantiatedTo(1)).toArray();
System.out.println("dominating set : " + Arrays.toString(solution));
System.out.println(model.getSolver().toOneLineString());
}
model.getSolver().printStatistics();
}
/**
* Creates an undirected graph of 6 nodes and 7 edges
*
* @return an UndirectedGraph
*/
private static UndirectedGraph createInputGraph() {
// creates a graph with 6 nodes (from 0 to 5)
UndirectedGraph inputGraph = new UndirectedGraph(6, SetType.BITSET, true);
// add 7 edges
int[][] edges = {{0, 1}, {1, 2}, {0, 3}, {1, 3}, {2, 4}, {3, 4}, {4, 5}};
Arrays.stream(edges).forEach(edge -> inputGraph.addEdge(edge[0], edge[1]));
return inputGraph;
}
/**
* Create a graph variable representing an induced subgraph of inputGraph
*
* @param model a choco-solver Model
* @param inputGraph an undirected graph defining the variable's upper bound
* @return an UndirectedGraphVar
*/
private static UndirectedGraphVar createGraphVariable(Model model, UndirectedGraph inputGraph) {
int n = inputGraph.getNbMaxNodes();
// --- graph lower bound : an empty graph
UndirectedGraph GLB = new UndirectedGraph(model, n, SetType.BITSET, false);
UndirectedGraph GUB = new UndirectedGraph(model, n, SetType.BITSET, false);
for (int i : inputGraph.getNodes()) {
GUB.addNode(i); // all nodes are possible
for (int j : inputGraph.getNeighborsOf(i)) {
GUB.addEdge(i, j); // all edges of inputGraph are possible
}
}
// create a graph variable with domain [GLB, GUB]
// any of its value will be a supergraph of GLB and a subgraph of GUB
return model.graphVar("g", GLB, GUB);
}
}